Random Scaling of Circles – Example 1.2

August 12, 2014

This second example introduces the concept of scaling objects, and also introduces the important concept of a Random number generator. Randomness is an important concept in many contemporary design expressions, but care should always be taken to find ways to manage or control randomness. Randomness for its own sake is not the goal. But you have to start somewhere….

This script also has four basic steps.

Step One – Setup Basic Structuring System

Like the last example, we need a starting structuring system. This time we’ll use a Hexagonal Grid of points. This could be a square grid as well, but I already used that in the last example! The hex grid functions similarly to a square grid although you’ll notice a 10×10 hexagonal grid actually has a rectangular proportion. You will also notice that the “P” output on the “HexGrid” component does not output the corner points of the cells, but the center points. So this time we do not need to use an “Area” component to find the centers.

Step Two – Draw Circles

A circle can be drawn in several ways in Grasshopper, but the most common is to identify just the center point and the radius of the circles. The radius doesn’t need to be that precise at this point since we will scale the circles up and down after this step.

Step Three – Setup Random Number Generator

We will scale our circles based on a range of scale factors. These will be produced by a random number generator. You should pay careful attention to this setup, since on this blog I use A LOT of random number generators. Randomness and controlling randomness are two essential concepts in complex form making systems. This particular example doesn’t have too much “controlled” randomness, unless you consider the range of scale factors a control.

A Random Number Generator always has three essential components:

The first (Letter R) is actually a Domain, so the letter D would be more appropriate, but I’m not programming this. A domain is mathematical term for a range of numbers (hence the R) and has a starting value and an ending value. For our scale factors, we might want to scale some circles up (factor greater than 1) and some circles down (factor less than 1). An acceptable range to achieve the results above might be .25 as the start of the domain and 1.4 as the end. Just a note, you never want to scale by “0” because this will make the geometry disappear and will generate an error.

The second is the number of random numbers (N). We could input a number here with a slider, but don’t do it! I almost always end up tying my random generator to a “List Length” component which measures how many items there are. So if I have 30 circles as in the example, it will generate 30 random numbers. Note you should measure the list after you graft or flatten it. In the example script where the data is grafted (see exercise one) the generator will only be generating one number!

The third component is the random number seed. Sliding this will reset the list of random numbers to another (pseudo) random number list. Sometimes this has a big effect but usually results look similar but not the same. We will see what this does soon.

Step Four – Scale the Circles

Now we hook our scale factors into the “Scale” component. Scale takes 3 inputs. The first is the Geometry we are going to scale, in this case, our circles. The second is the Center of the scaling, in this case, the center points of each circle.

The third input is the scale factor. This is generated by our random number generator. Note that in this first example, because of the way our data is structured, each row is getting the same scale factor. This may not be the affect you want. In which case, you have to change the data structure. Refer back to the first Example 1.1 for a more in depth discussion on data structuring.

if you don’t want the structure of rows in your random circle image, you should flatten the data structure with the center points after the grid is created. Now each circle gets its own random scale factor regardless of where the center point was originally created in the grid structure. Note, if you graft the points here, all circles will get the same scale factor.

If you don’t particularly care for the random distribution of scale factors, you can try out different random number seeds to see other variations. Each random number seed is not completely random. The computer has an algorithm for generating random numbers, so if you like one seed, say “Seed 100” and then you try out other ones, if you go back to “Seed 100” it will always generate the same results (assuming all other parameters stay the same)

*Note: There is another, perhaps easier way to do this script that doesn’t even use the “Scale” component. You can change the domain of your random number generator to output a list of radii instead of scale factors, and you can plug the results of your random number generator directly into the “R” port on the circle component.

Step Five – Coloring the Circles

As a last step, you can assign a color to the circles, as in the last example.

Variations

You can see in the results below some variations. This script doesn’t allow for TOO much variation, but you can play with the data structures, the “domain” or range of scale factors, and the random number seed.

As in the last example, examples in the first column have a flattened data structure, variations in the second column have a normal data structure, and items in the last column are grafted (so no variation, since each item is applied the same factor, being in its own list)

The three rows are just variations of various random number seeds. The variations are theoretically infinite but they look generally the same.

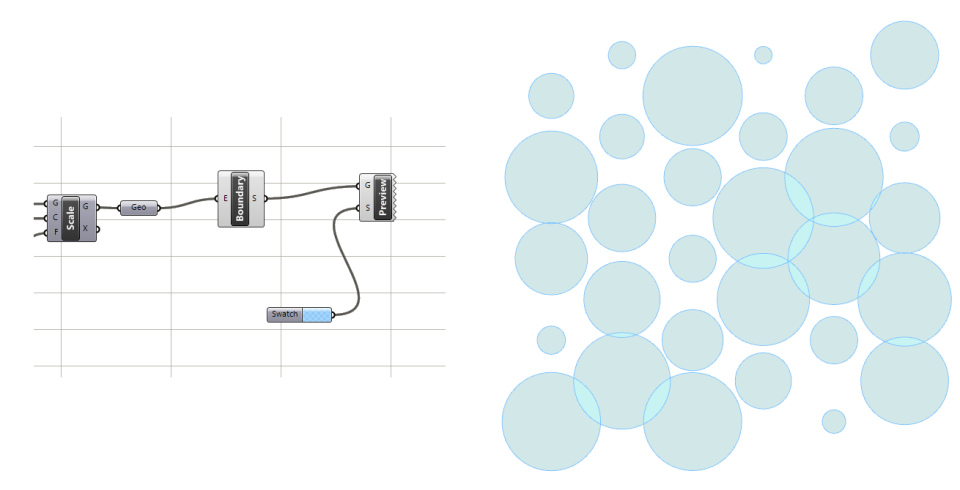
And here is (the correct) image of the grasshopper script…You can right click to change between “Flatten” “Normal” or “Graft” on the “Pt” container to get the various versions discussed above.

Click here to Download GH File

Post navigation

← Rotated Polygons on a Grid – Example 1.1

Jittery Rectangles – Example 1.3 →